How Well Does a Punnet Square Predict Actual Ratios?
In this lab you will make predictions using Punnet Squares, and then use pennies (or chips) to simulate the crosses. The results from the punnett square can then be compared to the actual data.
The trait you are looking at is the gene that codes for a short big toe in humans.T represents the dominant allele (short big toe), t is the recessive allele, long big toe. The photo shows a person with a short big toe. The following genotypes are possible. Fill in the phenotypes for them
Genotype / Phenotype
T T = ____________________________________
T t = ____________________________________
t t = _____________________________________
Part I
Use a Punnet Square to predict the ratio of offspring in a cross where the parents are both Tt (The Square is set up for you below)
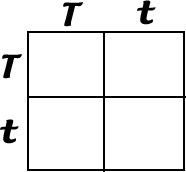 |
What proportion of the offspring (out of 4) will be: Short Toe______ Long Toe ______ *These are your predicted ratios. |
Now you will determine the actual ratios by using pennies (chips) to represent the crosses. You have two pennies. One one side of the penny is the letter T, on the other side is the letter t. This penny represents a parent that has the genotype T t. A second penny represents the other parent. One partner is going to play the role of female, the other will play the role of male. When the coin is flipped, you are determining what sperm or what egg is being donated to the match.
Practice flips. Flip the two pennies. The results show you what your offspring will be.
Did you get a TT, a Tt or a tt ? __________ What is the phenotype of your offspring (tall or short?) ___________
Procedure:
To determine Actual Ratios, you will flip your coins 100 times, recording in the table below how often each combination came up.(Use tally marks to record your data then summarize as a number)
| Gene Combination (Genotype) |
Tally
|
Total |
|
TT
|
||
|
Tt
|
||
|
tt
|
| Phenotypes |
Total
|
| Short toe (add TT + Tt ) | |
| Long Toe |
Since you flipped one hundred times, your totals above represent a Percentage. Your proportions from the Punnet Square in your prediction can also represent a percentage. ( 1/4 = 25 % 2/4 = 50% 3/4= 75% 4/4 = 100% )
Now compare your predicted ratios to your actual Ratios in the chart below.
| Predicted (from the Punnett Square in Part I) |
Actual (from the flips) | |
| TT | ||
| Tt | ||
| tt | ||
| Short Toe | ||
| Long Toe |
Would you consider the predicted values to be the same, close to the same, or not at all the same? ___________
Part II
You will repeat the procedure for parents that are Tt and tt
1. First make your predictions by setting up a Punnet square for the parents. (This one is not set up for you)
How many are predicted to be:
Short Toe______
Long Toe______
**Replace one of your pennies (chips) with a t t penny
Perform the flips with your new set of parents. Record your data in the table below
|
Tally
|
Total | |
| Tt | ||
| tt |
What percentage of your offspring are Tt _____ What percentage are short toes _______
What percentage of your offspring are tt _____ What percentage are long toes _______
Compare the Predicted Ratios of the cross to the Actual Ratios.
| Predicted (from Square) | Actual (from flips) | |
| Short Toe | ||
| Long Toe |
Analysis
1. Why are the Predicted Ratios rarely the same as the Actual Ratios?
2. Use a Punnet Square to predict the phenotypic ratios in this cross: T T x T t
Short toe _____
Long toe _____
3. If you used the coin toss method to determine the actual ratios, would it come out the same? Explain your reasoning.
4.What do the pennies or chips represent in the simulation?
5. When you toss the coin to see which side lands up, you are actually simulating what part of the process of sexual reproduction?
6. When you put the two coins that are flipped together, you are simulating what part of the process of sexual reproduction?
Other Resources on Genetics
Simple Genetics Practice - using mendelian genetics and Punnett squares
Peas, Please - practice setting up squares for basic Mendelian traits in pea plants (Key, TpT)
How to Solve Dihybrid Crosses - step by step guide on setting up 4x4 squares and determining ratios